冒泡排序

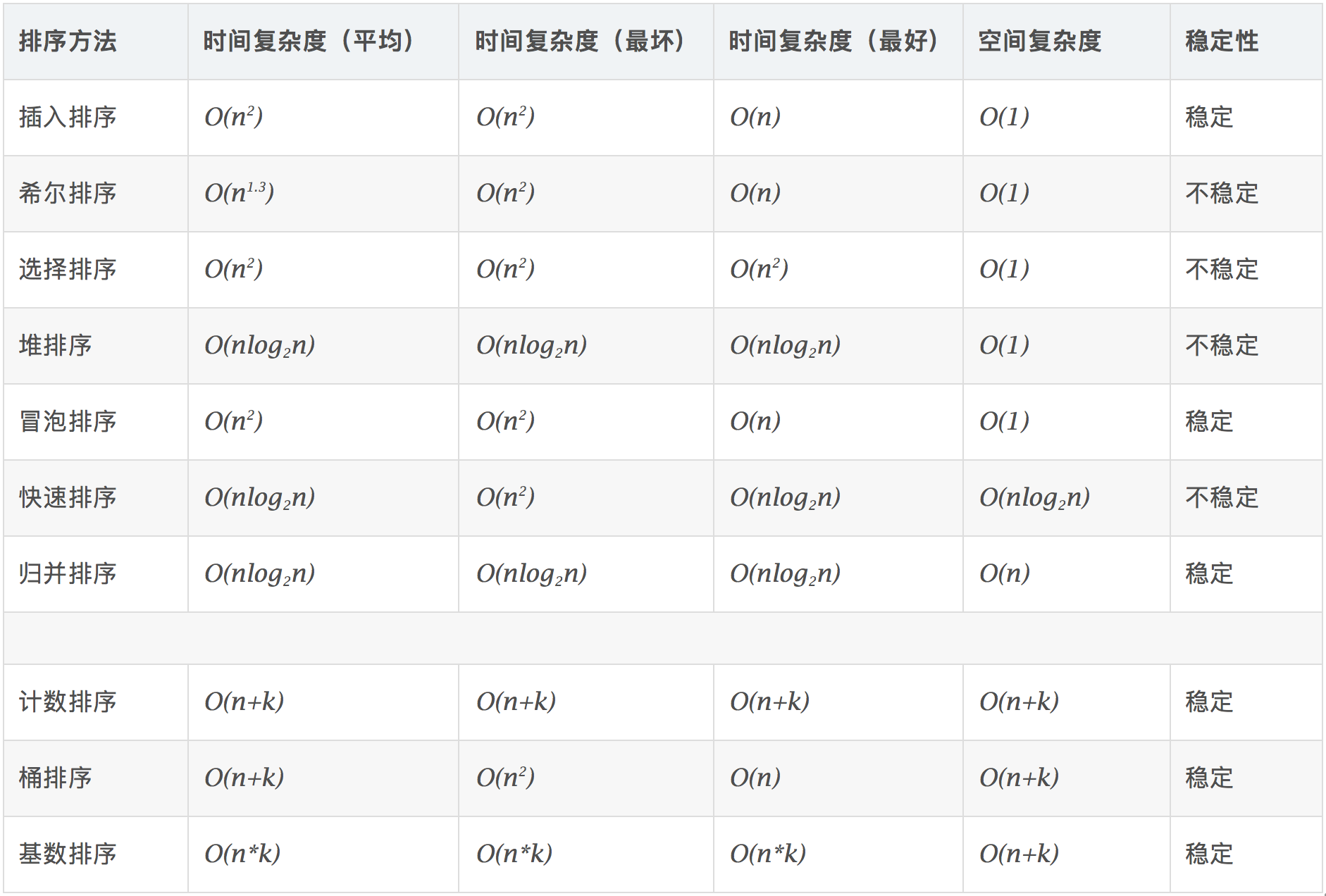
冒泡排序的思路：遍历数组，然后将最大数沉到最底部； 循环数组，比较当前元素和下一个元素，如果当前元素比下一个元素大，向上冒泡。 这样一次循环之后最后一个数就是本数组最大的数。 下一次循环继续上面的操作，不循环已经排序好的数。 优化：当一次循环没有发生冒泡，说明已经排序完成，停止循环。

• 最佳情况：T(n) = O(n)，当数据已经是正序时。
• 最差情况：T(n) = O(n2)，当数据是反序时。
• 平均情况：T(n) = O(n2)。

function bubbleSort(array) {
  for (let j = 0; j < array.length; j++) {
    const element = array[j];
    let complete = true;
    for (let i = 0; i < array.length; i++) {
      //比较相邻数
      if (array[i] > array[i + 1]) {
        [array[i], array[i + 1]] = [array[i + 1], array[i]];
        complete = false;
      }
    }
    //没有冒泡结束循环
    if (complete) {
      break;
    }
  }
  return array;
}

//简写
function betterBubbleSort(arr){
    const len =arr.length
    for(let i =0;i<len;i++){
        for(let j=0;j<len-1-i;j++){
            if(arr[j]>arr[j+1]){
                [arr[j],arr[j+1]]=[arr[j+1],arr[j]]
            }
        }
    }
}

/* 优化版
时间复杂度: O(n)
空间复杂度: O(1)
稳定
*/
const bubbleSort=function(arr){
    const len= arr.length
    if(len<2)return arr
    for(let i=0;i<len;i++){
        let flag=false
        for(let j=0;j<len-1;j++){
            if(arr[j]>arr[j+1]){
                const temp=arr[j]
                arr[j]=arr[j+1]
                arr[j+1]=arr[j]
                flag=true
            }
        }
        if(!flag) return arr
    }
    return arr
}

插入排序

将左侧序列看成一个有序序列，每次将一个数字插入该有序序列。 插入时，从有序序列最右侧开始比较，若比较的数较大，后移一位。

• 时间复杂度: O(n^2)
• 空间复杂度: O(1)
• 稳定

function insertSort(array) {
  for (let i = 0; i < array.length; i++) {
    let target = i;
    for (let j = i - 1; j >= 0; j--) {
      if (array[target] < array[j]) {
        [array[target], array[j]] = [array[j], array[target]];
        target = j;
      } else {
        break;
      }
    }
  }
  return array;
}

选择排序

每次循环选取一个最小的数字放到前面的有序序列中。

• 时间复杂度: O(n^2)
• 空间复杂度: O(1)
• 不稳定

function selectionSort(array) {
  for (let i = 0; i < array.length; i++) {
    let minIndex = i;
    for (let j = i + 1; j < array.length; j++) {
      if (array[j] < array[minIndex]);
      {
        minIndex = j;
      }
    }
    [array[minIndex], array[i]] = [array[i], array[minIndex]];
  }
}

归并排序

• 特性 分割数组时直接将数组分割为两个数组，合并时直接合并数组。 分治思想的践行：分割、合并

• 优点：思路简单，写法简单

• 缺点：空间复杂度略高，需要复制多个数组

   function mergeSort(array) {
      if (array.length < 2) {
        return array;
      }
      const mid = Math.floor(array.length / 2);
      const front = array.slice(0, mid);
      const end = array.slice(mid);
      return merge(mergeSort(front), mergeSort(end));
    }

    function merge(front, end) {
      const temp = [];
      while (front.length && end.length) {
        if (front[0] < end[0]) {
          temp.push(front.shift());
        } else {
          temp.push(end.shift());
        }
      }
      while (front.length) {
        temp.push(front.shift());
      }
      while (end.length) {
        temp.push(end.shift());
      }
      return temp;
    }

快速排序

数组分成三部分left、pivot、right，使left<=pivot，right>pivot 递归处理left 递归处理right 合并三者结果

const quickSort = array => {
    if(array.length <= 1) return array
    var pivotIndex = Math.floor(array.length / 2)
    var pivot = array.splice(pivotIndex, 1)[0]
    var left = []
    var right = []
    for (var i=0 ; i<array.length ; i++){
        if (array[i] < pivot) {
            left.push(array[i])
        } else {
            right.push(array[i])
        }
    }
    return quickSort(left).concat([pivot], quickSort(right))
}

//----快速排序----5行精简版

function quickSort(array){
    //设置边界
    if (array.length < 2) return array
    //找到基准值
    let pivot =array[array.length-1]
    // 比基准值小的，放到左则数组
    let left =array.filter((v,i)=>v<=pivot&& i!=array.length-1)
    // 比基准值大的，放入右侧数组
    let right = array.filter((v,i)=>v>pivot)
    //递归 左侧和右侧数组，结构并合并
    return [...quickSort(left),pivot,...quickSort(right)]
}

堆排序

堆是一棵完全二叉树，它可以使用数组存储，并且大顶堆的最大值存储在根节点（i=1），所以我们可以每次取大顶堆的根结点与堆的最后一个节点交换，此时最大值放入了有效序列的最后一位，并且有效序列减1，有效堆依然保持完全二叉树的结构，然后堆化，成为新的大顶堆，重复此操作，知道有效堆的长度为 0，排序完成。

完整步骤为：

• 将原序列（n个）转化成一个大顶堆

• 设置堆的有效序列长度为 n

• 将堆顶元素（第一个有效序列）与最后一个子元素（最后一个有效序列）交换，并有效序列长度减1

• 堆化有效序列，使有效序列重新称为一个大顶堆

• 重复以上2步，直到有效序列的长度为 1，排序完成

• 时间复杂度是 O(nlogn)

• 空间复杂度： O(1)

function heapSort(items) {
    // 构建大顶堆
    buildHeap(items, items.length-1)
    // 设置堆的初始有效序列长度为 items.length - 1
    let heapSize = items.length - 1
    for (var i = items.length - 1; i > 1; i--) {
        // 交换堆顶元素与最后一个有效子元素
        swap(items, 1, i);
        // 有效序列长度减 1
        heapSize --;
        // 堆化有效序列(有效序列长度为 currentHeapSize，抛除了最后一个元素)
        heapify(items, heapSize, 1);
    }
    return items;
}

// 原地建堆
// items: 原始序列
// heapSize: 有效序列长度
function buildHeap(items, heapSize) {
    // 从最后一个非叶子节点开始，自上而下式堆化
    for (let i = Math.floor(heapSize/2); i >= 1; --i) {    
        heapify(items, heapSize, i);  
    }
}
function heapify(items, heapSize, i) {
    // 自上而下式堆化
    while (true) {
        var maxIndex = i;
        if(2*i <= heapSize && items[i] < items[i*2] ) {
            maxIndex = i*2;
        }
        if(2*i+1 <= heapSize && items[maxIndex] < items[i*2+1] ) {
            maxIndex = i*2+1;
        }
        if (maxIndex === i) break;
        swap(items, i, maxIndex); // 交换 
        i = maxIndex; 
    }
}  
function swap(items, i, j) {
    let temp = items[i]
    items[i] = items[j]
    items[j] = temp
}

// 测试
var items = [,1, 9, 2, 8, 3, 7, 4, 6, 5]
heapSort(items)
// [empty, 1, 2, 3, 4, 5, 6, 7, 8, 9]

桶排序

桶排序是计数排序的升级版。它也是利用函数的映射关系。

桶排序 (Bucket sort)的工作的原理：假设输入数据服从均匀分布，将数据分到有限数量的桶里，每个桶再分别排序（有可能再使用别的排序算法或是以递归方式继续使用桶排序进行排）。

完整步骤：

• 首先使用 arr 来存储频率

• 然后创建一个数组（有数量的桶），将频率作为数组下标，对于出现频率不同的数字集合，存入对应的数组下标（桶内）即可。

• 时间复杂度：O(n)

• 空间复杂度：O(n)

let bucketSort = (arr) => {
    let bucket = [], res = []
    arr.forEach((value, key) => {
        // 利用映射关系（出现频率作为下标）将数据分配到各个桶中
        if(!bucket[value]) {
            bucket[value] = [key]
        } else {
            bucket[value].push(key)
        }
    })
    // 遍历获取出现频率
    for(let i = 0;i <= bucket.length - 1;i++){
        if(bucket[i]) {
            res.push(...bucket[i])
        }
	}
	return res
}

希尔排序

是简单插入排序的改进版。它与插入排序的不同之处在于，它会优先比较距离较远的元素

• 时间复杂度：O(n^2^)
• 空间复杂度：O(1)

function insertionSort(arr) {
    let n = arr.length;
    let preIndex, current;
    for (let i = 1; i < n; i++) {
        preIndex = i - 1;
        current = arr[i];
        while (preIndex >= 0 && arr[preIndex] > current) {
            arr[preIndex + 1] = arr[preIndex];
            preIndex--;
        }
        arr[preIndex + 1] = current;
    }
    return arr;
}

计数排序

计数排序不是基于比较的排序算法，其核心在于将输入的数据值转化为键存储在额外开辟的数组空间中。 作为一种线性时间复杂度的排序，计数排序要求输入的数据必须是有确定范围的整数。它是一种典型的拿空间换时间的排序算法

• 时间复杂度：O(n+k)
• 空间复杂度：O(n+k)

unction countingSort(arr, maxValue) => {
    // 开辟的新的数组，用于将输入的数据值转化为键存储
    var bucket = new Array(maxValue + 1),
        sortedIndex = 0,
        arrLen = arr.length,
        bucketLen = maxValue + 1

    // 存储
    for (var i = 0; i < arrLen; i++) {
        if (!bucket[arr[i]]) {
            bucket[arr[i]] = 0
        }
        bucket[arr[i]]++
    }

    // 将数据从bucket按顺序写入arr中
    for (var j = 0; j < bucketLen; j++) {
        while(bucket[j]-- > 0) {
            arr[sortedIndex++] = j
        }
    }
    return arr
}

基数排序

基数排序是一种非比较型整数排序算法，其原理是将整数按位数切割成不同的数字，然后按每个位数分别比较。由于整数也可以表达字符串（比如名字或日期）和特定格式的浮点数，所以基数排序也不是只能使用于整数。

• 完整步骤：

取得数组中的最大数，并取得位数； arr为原始数组，从最低位开始取每个位组成radix数组； 对radix进行计数排序（利用计数排序适用于小范围数的特点

• 复杂度分析

时间复杂度：基数排序基于分别排序，分别收集，所以是稳定的。但基数排序的性能比桶排序要略差，每一次关键字的桶分配都需要O(n)的时间复杂度，而且分配之后得到新的关键字序列又需要O(n)的时间复杂度。假如待排数据可以分为d个关键字，则基数排序的时间复杂度将是O(d*2n) ，当然d要远远小于n，因此基本上还是线性级别的 空间复杂度：O(n+k)，其中k为桶的数量。一般来说n>>k，因此额外空间需要大概n个左右

基数排序 vs 计数排序 vs 桶排序 这三种排序算法都利用了桶的概念，但对桶的使用方法上有明显差异：

• 基数排序：根据键值的每位数字来分配桶；
• 计数排序：每个桶只存储单一键值；
• 桶排序：每个桶存储一定范围的数值；

LSD Radix Sort
var counter = [];
function radixSort(arr, maxDigit) {
    var mod = 10;
    var dev = 1;
    for (var i = 0; i < maxDigit; i++, dev *= 10, mod *= 10) {
        for(var j = 0; j < arr.length; j++) {
            var bucket = parseInt((arr[j] % mod) / dev);
            if(counter[bucket]==null) {
                counter[bucket] = [];
            }
            counter[bucket].push(arr[j]);
        }
        var pos = 0;
        for(var j = 0; j < counter.length; j++) {
            var value = null;
            if(counter[j]!=null) {
                while ((value = counter[j].shift()) != null) {
                      arr[pos++] = value;
                }
          }
        }
    }
    return arr;
}